
現在、BBSに書き込みキーを設けています。「書き込みキー」欄に、「MYOMOTO」をカギカッコは抜いて、 半角、小文字で 打ち込んで書き込みをしてください。 このキーワードは時々変更されますが、その都度こちらにて報告します。

今更ですが、僕はGLSLデモはMicrosoft Edgeでしかテストしてません。Windows10デフォルトのブラウザがそれだからです。デフォルト以外の物をお使いの方はなんだかんだ言って自己解決する能力があると思いますから、OSの最初の設定をいじらなければ行けるようにしておけば間違いないだろうというポリシーからそうなってます。こんな誰も見ていないサイトで互換性など気にしていても仕方ないのです。
レイマーチングでリアルタイムデモを行う上で必要な事と言えば、やはりプリミティブをどう定義し、加工するか、という事です。折角ポリゴンしか使えない状態から曲面も(ある程度)自由に使えるようになったのですから、楽しまなくては。
正確に言うと曲面というより体積のある物体なんです。三角ポリゴンには体積が無く、基本的に表しかなかったのに対して、レイマーチングで扱うプリミティブには体積があり、裏と表、内側と外側があり、丸かったり尖ったりしています。穴をあけたり刻みを付けたりといった事ができますし、ひねったり互いにくっつけたりすることができます。但し、穴をあけたりくっつけたりひねったりといった変形を行うと距離関数が正確ではなくなるので正確な形状、特に実用的な精度で法線を得るためには物体の表面へにじり寄るように少しずつレイを進めていく必要があります。
現在、CSG(論理和以外)とくっつけるための演算(後で補足します)の相性が悪いので悩んでいます。CSGをかましても「距離0になる場所の位置」は変わらないのでレイをにじり寄らせれば一応形を描くことには問題ないのですが、「現在の地点から物体までの距離」は狂ってしまうのです。一方、くっつけるための演算は「現在の地点から物体までの距離」が正確でないと気持ちよくくっついてくれないんです。
また、CSGを使わなくても「物体までの距離は正確に返さないが距離=0になる面は正しい」という距離関数も作れてしまうので、レンダリング結果は正しくてもくっつけるとおかしなことになってしまう、というケースもあります。
例えば底面の半径r、高さhになる、原点に底面の中心を持つ底面付き円錐を以下のようなコードで定義するとします。関数名はとりあえずsdConeCSGとでもしておきます。
float sdConeCSG(vec3 p, float r, float h)
{
float ret;
vec3 pos = p - vec3(0,h,0);
float q = length(pos.xz);
//(0,h,0)に中心を持つ円錐面との距離(正確ではないが距離0になる面は正しい)
ret = dot(normalize(vec2(h,r)),vec2(q, pos.y));
//半空間y>=0で定義される物体と、↑との論理積
ret = max(ret, -p.y);
return ret;
}
円錐面と半空間の論理積を用いて、点pから円錐への距離を返す関数です。このsdConeCSGを使って距離を得ながらレイを飛ばすと一見正しく円錐が描かれるのです。

この関数は円錐に対する正確な距離を返していませんが、pが円錐の表面にあれば距離0を返すので見た目は正しいのです。一体どういうことなのか分りやすいように、sdConeCSGの返り値とpとの関係を以下に示しましょう。
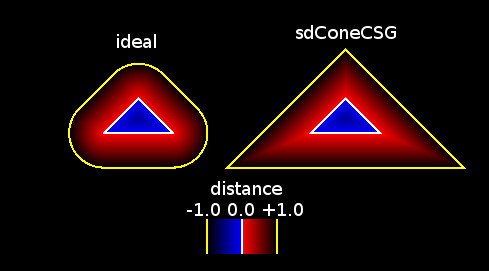
右の図がsdConeCSGのZ=0平面で切った時の返り値の図、左の図が同じ平面で切った時の円錐に対する実際の距離を示す分布図です。白線の所に円錐の表面ができ、黄色い線の所に円錐から距離1の面があるとして見てください。ご覧の通り、レンダリング結果としては正しく円錐が描かれていても、距離はおかしいのです。
一方、物体同士をメタボールのようにくっつける関数は以下のように書けます。iq大先生の関数をちょっと工夫して、二つの物体が対等にくっつくように改造したのがこちらの関数です。
float opBlend(float d1,float d2, float t)
{
float bfact = smoothstep(-t*0.5,+t*0.5,d1-d2);
return (mix(d1,d2,bfact));
}
この関数は、くっつけたい2つのプリミティブに対する距離関数の返り値を入力することで、2つのプリミティブ間の距離がt以下になっている時は滑らかにくっつけることができます。例えば、正確な距離を返す球と直方体を定義するsdSphere,sdBoxという関数があったとして、そいつら同士に使うと以下のようになります。

d = opBlend(sdSphere(...), sdBox(...), 1.0);
球は箱型に変形し、箱は球型に変形してくっついていますね。自分の都合ばかり考えず、相手に合わせてお互いに自分の形を変える、これが融和という物です。昨今の国家間、民族間の軋轢に対するソリューションが見事に示されています……なんてね。「メタボール」と言うと球状でないとダメな気がしますが、この関数さえあれば球だろうと直方体だろうとくっつきます。しかし、さっきの円錐のように正確な距離を返さないプリミティブに使うとどうなるかというと

d = opBlend(sdSphere(...), sdConeCSG(...), 1.0);
球が深々と抉られてしまいなんだか痛々しい変形結果となってしまいました。opBlendは距離しか見てない関数なので距離がおかしくなれば当然くっつけた結果もおかしくなるというわけです。どんな物体でも容易にくっつけられる魅力的な関数と思っていたのにこれでは台無しです。opBlendを取るかそれとも全てのプリミティブに正確な距離を期待するか、悩みどころになってしまいますが別にゲーム作成エンジンを作りたいわけでもないので「何を描きたいのか」という事に常に焦点を合わせてケースバイケースで柔軟に対応していくのが良いと思います。実は前回の豚の耳とか足に使われている円錐はこの関数で作られていまして、そのため耳とか足が胴体とあんまり柔らかくくっついてないんです。
……と終えてしまうのも今回何もしてない感が強いので、opBlendのくっつき方だとなんといいますか、お互いのスキマを埋めるように凹みあいながら遠慮がちにくっつている感があるので、もうちょっとお互いカモンカモンな感じでアグレッシブにくっつく関数を作ってみようとしたら、魔法のザブトンを介して吸い込まれるような変なエフェクトが出来てしまったので置いておきます。超高速で衝突する様子の表現なんかにはいいかもしれませんよ??
//dir = 0.0~1.0で与えられる「くっつく方向」0.5:対等 0:d1→d2 1:d2→d1
//speed : 0.0 ~ 1.0未満で指定。 大きいほど変形しまくる
float opSonicBlend(float d1, float d2, float t, float dir, float speed)
{
float bfact = smoothstep(-t*(1.0-dir),+t*dir,d1-d2);
return min(d1,d2) - mix(d1,d2,bfact) * speed;
}
Hayase Taku(SANDMAN)