
現在、BBSに書き込みキーを設けています。「書き込みキー」欄に、「MYOMOTO」をカギカッコは抜いて、 半角、小文字で 打ち込んで書き込みをしてください。 このキーワードは時々変更されますが、その都度こちらにて報告します。

かぜのなかのすーばるー
豚はどこへ行くのでしょうか、見送られることもなく
あれ、太陽近すぎない?
というわけで、今日はボリュームライト(ゴッドレイ)をやってみました。パーリンノイズとかは使ってないのですがサンプリング間隔が長いせいで微妙なモクモク感があります。ポリゴン製のゲームで良く使われるスクリーンスペースでのラジアルブラーによる近似でもなければそもそもポリゴンなんて画面の枠をつくるための2トライアングルしか使ってないのでケレン味のあるシャキッとした影を出そうとするとサンプリング間隔を短くしないといけないため猛烈に重くなるし……とかなり工夫の要るエフェクトのようです。
コンパイル後のシェーダーのサイズがかなり大きくなるようで、おそらくIEでは動きません。ChromeやEdgeなど、IEよりはWebGLに強いと思われるブラウザで見てやってください。
とりあえず原理だけ聞いてなんとなく式を考えて実装してみたので合ってるのかいまいち自信が無いのですが、「こういう式だとこういう見た目になるよ」程度に読んでやってください。
光の筋を見せるテクニックであるボリュームライトの原理というのは空間上のある点を描くにあたり、光がどれだけ物体によって遮られているのか考慮するというただそれだけの事です。光を見せるために影の計算を細かくする、逆説的ですがそういう事なのです。腕の良いカメラマンは影を作るためにライトを使うように、気の利いたシェーダ書きは、光を見せるために影を計算するのです。

そもそもなんで光の筋が見えるのかというと、塵などのやや大きめの分子によって光が散乱される、いわゆるチンダル現象によるものである、という所まではご存知の方も多いと思います。窓から光が差し込んでいるのが見える!ああ、部屋が埃だらけなんだな!と判る訳です。風情も何もあったものではないですね。
一応、今回は見た目が劇的に変化しやすいよう、点光源を1つだけ置いた空間を仮定します。空間内は一様に塵っぽい粒子がたちこめているとします。塵によって光が散乱され、その様子をレンダリングすることで光の筋が見えるという感じで。
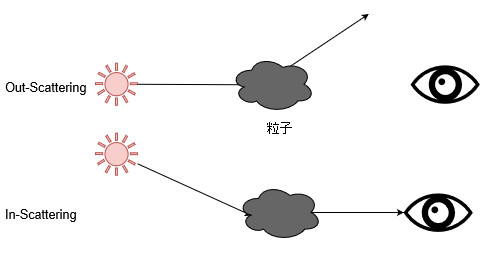
さて、空気に漂う粒子と光がぶつかると、粒子によって光は「吸収」されたり「散乱」されたりします。吸収についてはあまり考えなくてもいいらしいのでここでは散乱についてだけ考えましょう。散乱する方法も2通り考えられまして、視線以外の方向から視線方向に光が上手い事曲がってくれる「in-scattering」と、折角視線方向に飛んでいた光が違う方向にそれてしまう「out-scattering」の二通りがあります。
空間内に粒子が一様に分布していると仮定すると、直線上を進めば進むほどin-scatteringによって光が足しこまれていきます。これには視線の外から飛んでくる光を視線方向に上手く屈折してくれる確率を求めないと行けませんから、今回はMie散乱に従うと仮定しました。Mie散乱の式というのは以下の通りで、光が射し込んだ方向より\(\theta\)だけ回転した方向へ光が出ていく確率\(\Phi_M\)を求めることが出来ます。\(g\)というのは係数で、-1より大きく0以下の負の値を取り、-1に近いほど鋭い指向性を示します。つまり、あまり光を散らかさない粒子になります。逆に0に近い値にすると指向性が無くなって全方位に均等に光を散らすようになります。今回の作例ではgがよほど-1に近くないと劇的な変化はないですし、-1に近くなっても見た目に面白くなかったのであんまり真面目に計算しなくても良い気がします。むしろRayleigh散乱の波長依存性とかの方を真面目にやった方がよかったかなあ……
\[ \Phi_{M}(\theta) = \frac{1-g^2} {4\pi (1+g^2-2g \cos \theta)^{\frac{3}{2}}} \]で、ボリュームライトを実現するにはin-scatteringに対する工夫がキモになります。空間内に粒子が一様に分布しているモデルを仮定しましたが、今回は「周りにある物体が光を遮る効果を無視しない」事が重要なのです。いつも通りレイマーチングではカメラから画面上のピクセルに相当する位置に向かってレイを飛ばしてそのまま物体の表面か遠方クリッピング面の彼方までレイを飛ばしますが、物体の表面にぶつかってもぶつからなくてもレイが動いた軌跡をとりあえず何分割かします。分割しすぎると重くなるのであんまり細かく分割できません。ともかく、分割した軌跡上の各点を\(\vec{s_i}\)と名付けます。\(i\)は0~分割数-1の値を取ります。今回の作例では最初に飛ばしたレイを物体とぶつかった場合はその手前、ぶつからなかった場合はカメラから15mの地点から分割を初めて32等分に分割しています。カメラから遠い所は粗く分割するなど工夫するとパフォーマンス的には良いと思います。最初はGeForce GTX970を積んだ古いデスクトップマシンで書いてたので128分割だったのですが、NUCでも動かしたら重くてまともに操作できなくなってしまったので32分割に減らしました。
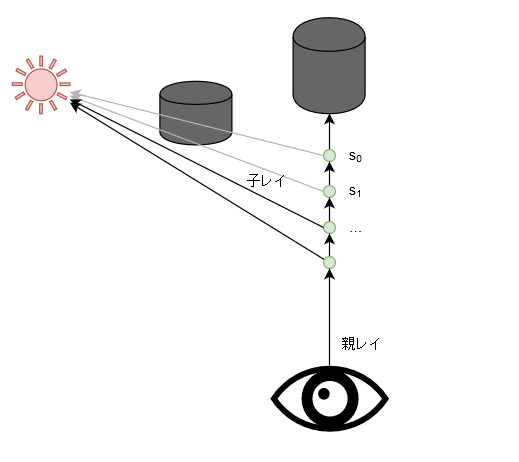
図がシュールですみません…… GIMPにどうしても慣れられなくてdraw.ioをありがたく使わせていただいているのですが、まだ慣れないものでして。でも見た目はともかくdraw.ioの生産性の高さは凄いですね!使い方を調べなくてもこのくらいの図なら2~3分でサクサクと描けました。
さて、レイの軌跡上のある点\(\vec{s_i}\)から光源に向かってさらにレイを飛ばします。子レイとでも呼びます。子レイはなんのために飛ばすのかというと、親レイの軌跡上の点と光源の間に物体が割り込んでないか知るためです。物体が割り込んでいたら遮蔽率\(C(\vec{s_i})=1\)とし、割り込んでなかったら遮蔽率\(C(\vec{s_i})=0\)としましょう。現実に即したモデルを考えると光の波長レベルの細かい事まで考えなければ遮蔽率は1か0しかありえないのですが、そうしてしまうと軌跡の分割時の粗さが仕上がりにモロに影響を与えてしまうので、「わりと惜しい」位置を光がかすめていったときは0と1の間を取るように工夫します。今回は、子レイを飛ばした時の物体への最短距離を\(d_{min}\)として記録し、\(e^{-k d_{min}}\)(\(k\)は大きいほど影がシャープになる係数)を遮蔽率としてみましたが、わりと良好な結果が得られました。
子レイを飛ばすときの実装上の工夫として、影を作るためのモデルは表示用のモデルと別に、一個の楕円体を置くことにしました。豚だとプリミティブが10個以上あるので、楕円体一個にしてしまえば単純に1/10くらいの計算コストになるからです。こういう小細工はしたくないのですが、今回はさすがに見た目と重さのバランス的にこうしています。というか豚モデルのまま影を作ろうとするとコンパイル後のシェーダがデカくなりすぎるのかEdgeでもコンパイルできないことがしばしば起きましたので……

さて、レイの軌跡上の点\(\vec{s_i}\)において、光源から受け取れる光の量は、点光源の位置ベクトルを\(\vec{l}\)、全光量を\(A\)とすると以下のようになります。
\[ \frac{(1-C(\vec{s_i})) A}{4 \pi |\vec{l}-\vec{s_i}|^2} \]こいつがそのまま視点に届くかというとそうではなく、上手い事\(\vec{s_i}\)にある粒子によって視線の方向に曲がってくれないといけません。それには
目に届く光量をLとすると、雑ですが\(\vec{s_i}\)から\(\vec{s_{i+1}}\)まで動きながら受け取れる単位長当たりの光量\(\frac{dL}{dx}\)を以下のように近似してしまいます。よほどの高性能GPUを前提にしないと\(\vec{s_i}\)って結構間隔が長くなっちゃうのですが、その間隔は「十分短い」のです(血涙) 一応、苦し紛れに線形補間するバージョンも作ってみたのですが、やはりサンプリングの粗さを補うことはできませんでした。 ともかく、区間\(\vec{s_i}\)~\(\vec{s_{i+1}}\)の長さを\(d\)、各点における光量を\(L(x), 0 \le x \le d\)として、区間の初めである\(\vec{s_{i}}\)における光量を\(L_i(0)\)としましょう、
\[ \frac{dL_i(x)}{dx} = \frac{\beta \Phi_{M}(\theta) (1-C(\vec{s_i})) A}{4 \pi |\vec{l}-\vec{s_i}|^2}で一定 \]要するに注目している区間の間、光源からin-scatteringで足しこまれる光量は全く同じで続くと仮定するわけです。in-scatteringだけ考慮するなら動いた距離を掛けるだけです。次に、out-scatteringのための計算を追加します。ここで上記のin-scatteringによって光が足しこまれつつ、out-scatteringによって単位長さ当たり\(\beta L_i(x)\)の光が失われるとすると
\[ \frac{dL_i(x)}{dx} = -\beta L_i(x) + \frac{\beta \Phi_{M}(\theta) (1-C(\vec{s_i})) A}{4 \pi |\vec{l}-\vec{s_i}|^2} \\ \]これを解いて
\[ L_i(x) = L_i(0) e^{-\beta x} + (1-e^{-\beta x})\frac{\Phi_{M}(\theta) (1-C(\vec{s_i})) A}{4 \pi |\vec{l}-\vec{s_i}|^2} \\ \therefore L_i(d) = L_i(0) e^{-\beta d} + (1-e^{-\beta d}) \frac{\Phi_{M}(\theta) (1-C(\vec{s_i})) A}{4 \pi |\vec{l}-\vec{s_i}|^2} \\ L_{i+1}(0) = L_i(d) \]この計算を、視点から一番遠い区間から近い区間に向かって、\(L_i(d)\)を次の区間の\(L_{i+1}(0)\)として繰り返していけば目に届く光量(の雑な近似値)が求まります。最初の区間の\(L\)の初期値である\(L_0(0)\)は、今回の作例では物体にレイが当たった場合は物体の表面の色にし、そうでない場合は環境色(真っ黒)にしてみました。in-scatteringは区間ごとにサンプリングした値ということで離散的なのにout-scatteringは座標から連続的に求まるので、なんだかちぐはぐな感じもしますが、カメラに近い位置への影の落ち方を見るとout-scatteringだけでも連続的に計算してやるのは有意義なようです。最初は微分方程式を解くのを面倒くさがって、各\(s_i\)ごとに\(e^{-\beta_M d}\)を掛けるようにしていたのですが、上の式の方が僕の主観的には良い結果が得られました。WolframAlpha様様です。ちなみにリンクにある式はin-scattering分を線形補間した場合の計算式です。ソース内に残骸が残ってます。単なる線形一階微分方程式なので手計算でも簡単ですが、僕は計算ミスが多いので紙の節約にもなってすごく助かってます。
実装の仕方を鑑みるにボリュームライトはフォグの仲間と考えるとよさそうですね。梅:expフォグ、竹:Rayleigh/Mie散乱、松:ボリュームライトというような感じでこう。今回の作例では上記の計算を通しているだけでexpフォグをさらに掛けていたりはしてないのですが、いい感じにスモーキーになりますね。豚のライティングには簡単にLambertディフューズとアンビエントオクルージョンだけやっています。
ところで、円錐のための距離関数を手直しして豚の耳と足をマシにしてみました。距離が正確に取れるプリミティブなら距離関数の返り値に増減するだけで丸く太らせたり痩せさせたりできるのでついでに丸めてみましたので、多少は可愛さがアップしたかもしれません。あと、足も無理やり動かしてみました。このどうでもいい修正のためにGWの半日を費やしてしまいました。どうせ出かけるお金も無いので実に有意義なGWになりそうです!
Hayase Taku(SANDMAN)