現在、BBSに書き込みキーを設けています。「書き込みキー」欄に、「MYOMOTO」をカギカッコは抜いて、 半角、小文字で 打ち込んで書き込みをしてください。 このキーワードは時々変更されますが、その都度こちらにて報告します。
納得がいかない。
なんとなく使ってはいるもののクォータニオンについて完全に理解している気がしないのはなぜなのか? 「クォータニオンは3Dゲームにおいて姿勢を制御するために便利なクラスです」で終わりというのは あまりにも寂しい。複素数について高校数学で扱う範囲よりほんの少し足を伸ばすだけで、 複素関数における一致の定理やそこから導かれる解析接続について理解でき、\[1+2+3+\cdots=-\frac{1}{12}\]という不可解な数式について 違和感がなくなるなど、とてつもなく味わい深い世界に入れるように、より深くクォータニオンについて考えることで もっと楽しいものが作れるようになるかもしれない! 実にクォータニオンに初めて触れてから20年ほど経ちましたが、いまさらそれをほじくり返してみようかと思い立ちました。
まず僕がクォータニオンについてなんとなく使えはするけど理解できてないところというのは以下の通りです。
順番に考えるとしましょう。
いきなり数学じゃなくて歴史です。何事も「どういう経緯でそんな概念が生み出されたのか?」 という基礎的な事実は確認しないといけません。まずは、クォータニオンの前身と言える複素数の歴史について紐解いてみましょう。 「え?そこから?」と思うかもしれませんが、ココが、というかむしろココこそが意外に重要な話です。
負の数の平方根について言及している文献となると、古代ギリシアにまで遡ると言われますが、 分かりやすいので入門用記事として重宝させていただいているニコニコ大百科の記事によると 複素数の歴史は、1545年はイタリアの数学者であるカルダーノが三次方程式の解法を示すために導入した事から 始まるとされています。虚数解というものは二次方程式にも存在しますが、それまでは完全に無視されていたんでしょうか。 当時は負数やゼロさえ実在しない数として扱われ、虚数というネーミングも後のデカルト(彼は1596年生まれ、1650年没の人物です) によって「そんな数ねーから」というようなネガティブな文脈で与えられたと言いますから、 「有るのか無いのかなんかよくわからんけどそういうモノを仮定しないと上手く書けないから、 仕方なく虚数的な?コンセプトを盛り込んどく?」という感じでカルダーノも使っていたんでしょうね。 なにしろ当時の理解では虚数は図示できないので、見ることが出来ない。見ることが出来ないなら無いんじゃね? となってしまった。
しかし、「そんな数ねーから」扱いされていた虚数がいかにして歴史に残ったんでしょうか? そんな数は無いというなら役にも経ちませんし考える必要もないはずです、と、僕の高校時代の古文の教師も言ってました。 けれど、この言葉は僕に絶大なインスピレーションをもたらしました。「ありもしない数を勘定して何になるんだ?」 と言われてもハミルトンやマクスウェルの名前を挙げるまでもなく、それでメシを食ってきた数学者や物理学者は 歴史上山のように居ただろうし現代においても幾らでも居るだろうということは当時の僕にもよく分かっていました。 彼らは詐術師の類などではなく、人類の歴史に燦然と輝く業績を打ち立てた巨魁も大勢含まれる集団ですから、 「一見ありもしない、役立たない概念についても深く考察をすることで天地をひっくり返すような凄いことが出来るかもしれない」 という一種の確信を抱くことになったのです。……と、話が完全に脱線しました。
ともかく、「図示できないようなモノを信じるわけにはいかない」というのが当時の数学の世界での信条だったようで その後の、ウォリス(1616年~1703年)による虚数の幾何学的表示への挑戦 (当時の受け入れられ方や理論の矛盾などから成功したとは言えないものだったそうです)などを経つつ200年の歳月が流れました。 1745年、ライプニッツとベルヌーイの往復書簡集が刊行されたそうです。 ベルヌーイは一族がかりで数学や物理などで山のように業績を上げているので単に「ベルヌーイ」とだけ書くと誰のことだかわかりませんから、 1667年誕生~1748年没のヨハン・ベルヌーイの事です。かのレオンハルト・オイラーの師でもあります。 書簡の相手であるライプニッツは1716年に没したので、この書簡集はライプニッツの没後であり、 ヨハン・ベルヌーイ本人の晩年に刊行されたことになるのですが、その内容は負数と虚数の対数に関する論争だったそうです。 この頃にはすでに虚数というものを勘定すると色々面白いぜ?という事が最先端を走る人たちには分かっていたということです。 その少し後の1748年、かの美しきオイラーの公式 \[e^{ix}=\cos x + i \sin x\] が出版・公表されます。(とはいえ、最初に発見したのはロジャー・コーツによる1714年の出来事だったそうです)
虚数の図示に初めて成功したのはさらに50年ほど後、ノルウェーのヴェッセルによる1797年の論文だそうで、 複素数を平面に図示するというアイディアに、ついに到達しました。同時期に複素平面についての着想を得ていたのは フランスのアルガン、そしてあのガウスだそうです。なので、フランスでは複素平面の事をガウス平面ではなくアルガン平面と言うそうです。 実にカルダーノから250年の歳月を経て、複素数は平面上に図示できるという事が公表されたのです。 数というものはそれまで数直線という直線の上に並べられて、「数っていうのは直線からハミだしたりしないんだ、 一次元の存在なんだ」という理解から、「実は複素数って言って二次元の数があるんですよ」という話になってしまいました。 一次元だと思っていたあの子が二次元の存在だったなんて。一気に夢が広がってしまいました! 「なんか有るのか無いのか良くわからないけどこういう概念を使っときます」から「実は二次元キャラです」 まで実に250年!壮大な物語でした -完-
いや、終わりません(セルフ突っ込み) ガウス平面の由来にもなっているガウスの無双状態について色々書くべきかもしれませんが、 ガウス達の様々な業績によってもはや虚数は「概念上にしか無い、良くわからない厄介者」ではなく「数学にとって無くてはならないツール」 へと変化していきます。我ながらザックリすぎる感がありますがガウスの業績というのはそのくらい多すぎるんです。 特に我々としては平面上の座標を示すのに使えるというのはデカいです。 けれど「え?でも?そんなのベクトル使えばいいじゃん?」とも思うでしょう。 当時、数学の世界にベクトルは無かったんです。ええ、なかったんですとも。 18世紀頃から天文学の分野でベクトルという用語自体は使われていたらしいのですが、 一体どういう概念として使われていたのか詳細については辿り着けませんでした。 ともかく、数学における現代的なベクトルの概念が確立するのはギブス(1839年-1903年)らによって ベクトル解析学が興る19世紀終わり頃になってからなので、わりと最近の話なんですね。 そもそもガウスは独自にクォータニオンに相当するものをハミルトンより25年も早く発見していたそうですが、 特に公表することもなかったので長らく日の目を見なかったのだそうです。えぇ……。
そんなガウスの弟子の一人に、メビウス(1790年-1868年)が居ます。メビウスというと「変な輪っかを考えた人」として非常に有名ですが、
彼は同次座標系、そしてメビウス変換を編み出した人物です。
同次座標系……これも「なんとなく使ってるけど実は良くわからない」概念じゃないですか?
しかも、Unityにおんぶにだっこだとほとんど意識しなくても良くなります。
とはいえご安心ください、僕もそうです!ですから、ちょっと寄り道して同次座標系についても見てみましょう。
クォータニオンの発見と比べれば地味かもしれませんが、これも本当に素晴らしいアイディアです。
Wikipediaなどでメビウスの生涯について調べても何故か全くかすりもしないので、あまり歴史的な側面については分からなかったのですが、
同次座標系(英語版Wikipedia)について調べると
1827年の著作でメビウスが公表したと書いてあります。
同次座標というのは生立ちからして射影変換に使うために考えられた物だそうで、まさしく今日の僕らが使っている用途に当初から使われていたモノです。
以上!
では寂しいので、もうちょっと触れると、今日において同次座標系を取り入れるメリットというのは御存知の通り、
同次座標系を取り入れることでこういうメリットがあって、とりあえずメリットがデカいので受け入れざるを得ないという所ですが、 おそらく同次座標系についてスッキリしない点というのは、同次3Dベクトルには4つ数があるけど4次元なの?3次元なの?という所です。 なんか3次元の計算に使ってるけど実は4次元だったりしない?と思った事ないですか?? 同次三次ベクトルが三次元なのか、四次元なのかという事は、実は捉え方によります。 ここからしばらくは僕の独自解釈ですから話半分に聞いていただきたいんですけれど、御用とお急ぎのない方はしばしお付き合い願いとう御座います。
まず、1つ目の捉え方として同次三次ベクトルはあくまで三次元+1スカラーという捉え方。 これはいつものデカルト座標系との違いを意識すると幾分スッキリすると思います。 というのも、デカルト座標系では「同じ位置にあるものには同じ座標、違う位置にあるものには違う座標」が必ず割り当てられます。(余談ですが極座標系もそうでしたね) 一方で、同次座標系では「同じ位置にあるものでも無数の違う座標が割り当てられる」という事になります。それでいいんです。 その重複を許している、冗長性があるから数が一個増えているのです。 そして、増えた数であるW成分が、座標に対する「重み」として働いています。 一つの同次三次元座標は、間違いなく三次元のデカルト座標に対応する座標一つを示していますが、一つのデカルト座標に対応する同次座標は無限に作れます。 僕らはいつも座標とかベクトルとか空間とかいう言葉をホイホイ使いますけど、暗黙のうちにデカルト座標だし、暗黙のうちにデカルト座標を格納したベクトルだし、 デカルト座標で位置を表現できる空間というものをイメージしがちです。他の座標系を使う時は、そのイメージから一時離れる事も重要だという事ですね。
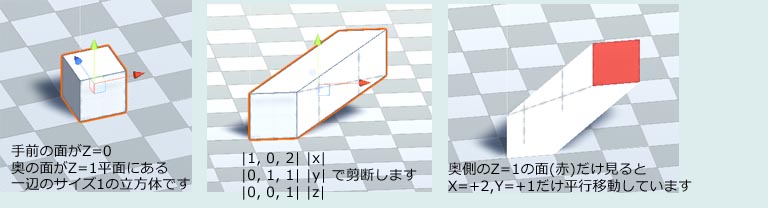
では、同次三次ベクトルは四次元のデカルト座標についての情報は持っていないのかというと、 ここから2つ目の捉え方についてのお話になるんでございます。 同次三次ベクトルを「四次元デカルト空間を三次元デカルト空間に射影するためのツール」として捉えると同次三次ベクトルはW成分を逆数にすると 四次元デカルト空間での座標をそのまま(あるいは画角などを調整するために線形変換の1回くらいは必要になるかもしれないけど)格納していると言えるからです。 「なんだよやぶからぼうに、俺は4次元のことになんて興味無いって言ってるだろ、余計な次元の押しつけなんてよしてくれよ」 と思うでしょうけれど、まあもう少し、ちょっとですから聞いてください。 3x3の行列を使うと2次元の点の平行移動が出来ます。同様に4x4の行列を使うと3次元の点の平行移動が出来ます。 これはどういうことなのか、計算すればすぐ分かりはするんですけど、幾何学的にどういう意味なの?と思ったことないですか? これはですね、「1つ上の次元で剪断(せんだん)をすると元の次元での平行移動が出来る」ってことなんです。 あんまり使わない気がする剪断と更に使ったこともない気がする四次元デカルト座標ですが、実はWを逆数にしながらとはいえ毎日使いまくっていたのです。 文章だと雲を掴むような感じがすると思いますから、試しに三次元で剪断をすると二次元でどう表示されるのかという下手くそな絵を作ってみました。

「行列で平行移動がしたいからなんか数を足した」のではなく意外と奥深い、それこそZ軸では表現できないほど奥深いけれどシンプルな理由がありまして、 僕らは実に毎日四次元の計算をしていたのです。 他の座標系を使うときも、元のイメージを完全には離さず2つのイメージを同時に持つと、奥ゆかしい世界が見えてくるのかもしれません。 僕らの知っている3Dゲームに登場するグラフィックも、四次元で見るとW=0空間からW=1空間に伸びる剪断で作った「みにょーん」とした図形だらけに見えるのかもしれません。 四次元人達はその様を滑稽に捉えているのかもしれませんよ??
以上の二つの捉え方は、どっちが正しいとかどっちが間違っているという話ではなく、どっちも正しくて共存できると僕は思っています。 俺は三次元のアプリケーションのプログラミングに集中したいんだ!二次元でも十分なのに四次元とか知らねぇ! という時は前者の捉え方を採用すればいいでしょうし、それだけではもしも行き詰まってしまった時や、 何か理解し難い計算についての幾何学的解釈に基づいたヒントがほしい時なんかは 後者の捉え方を思い出していただければいいんじゃないかと思います。
さて、少し寄り道をしましたが、ガウス平面という概念の普及により、二次元で満足する人たちは幸せな生活を享受できるようになりました(語弊あり) しかし、時は19世紀も中頃、ファラデー(1791年-1867年)らの業績により、電磁気学などの新しい物理学の分野が勃興してきました。 そうなってくると二次元では飽き足らず、三次元の問題も扱えるような数が欲しくなってきます。 まあ二次元くらいだったらxとyだけですからベクトルが無いからと言ってもx成分とy成分についていちいち書いたって良いでしょうけど 三次元となると相当面倒ですから「三次元の数」があれば一発で書けるので助かりまくる事が想像できます。 そんな実用面はさておくとしても、とにかく二次元がOKなら三次元も!となるのは必然的な流れです。
さあ、ここでやっと登場するのが我らがハミルトン(1805年-1865年)です。当然の成り行きとして「三次元の数だからiとjをくっつけた数!」 と考えるわけですが、そんなものはない。何故無いのかは後述します(勿体ぶるわけでは無いんですが) ともかく様々な試行錯誤紆余曲折を経て1843年、ついに「kをくっつけて4つにすれば行ける!」とクォータニオンの概念に到達します。 以来彼はクォータニオンに取り憑かれてその後の生涯をクォータニオン関連の著述に費やすのですが、 当時の数学者であるハーシェルや親友であったド・モルガンにすら「難解である」と評され、後に四元数の基礎という著作も成すのですが、 長すぎて生前に出版されず、死去の翌年の1866年になってようやく出版されたそうです。 散々勿体をつけてやっと登場した世紀の天才ハミルトンなのになんだか冴えない話みたいになってしまい、悲しい気持ちですが、 新潟工科大学 竹野茂治先生による「数学に関する質問とその背景の数学」によれば ハミルトンはクォータニオンだけでなく、ベクトルという名称を数学に用いだし、スカラーという言葉を考えた人物でもあります。 実にクォータニオンのW成分をスカラー部分、XYZ成分をベクトル部分と呼んだのが数学史におけるベクトル・スカラーという概念のそもそもの始まりだったのです。 ベクトル・スカラーからクォータニオンが生まれたのではなく、順序が逆なんですね。 クォータニオンを打倒した怪物を自分で作ってしまっていたとは! 確かにベクトルの概念すら無い時代にいきなりクォータニオンなどと言われたら余程の頭脳の持ち主でもないと全く理解できないでしょう。 ベクトル積・スカラー積というのもハミルトンの考えた用語で、クォータニオン同士の掛け算をした後に出来る W成分の値が「スカラー積」XYZ成分の値が「ベクトル積」なんです。試しにクォータニオンのW成分に0を代入したもの同士を乗算すると『!』 となりますから実際やってみてください。 今の今まで僕も「内積っていうのはなんか、そういう計算をすることが多いし、だからそういうのに特別な名前を付けたんじゃないかなぁ?」 とドローンとした解釈をしていたのですが、クォータニオンの乗算から生まれた出でたときからスカラー積はスカラー積だったのです。
さて、確かにクォータニオンの方が三次元ベクトルより何かと美しいし作者も人生を捧げるほど愛してやまなかったのですが、 いかんせんとっつきにくい。ぶっちゃけスカラー部とかいう良くわからないモノがくっついてて邪魔です。 京都大学から公開されている蔵書、「数理解析研究所講究録 1317巻 2003年」より、立教大学名誉教授 公田 藏先生 著 「日本の数学教育とベクトル この百二十五年」によりますと、ハミルトンの業績に早くから注目・傾倒していた Peter Tait(1831年-1901年)の勧めによってマクスウェルは1873年に著した「電磁気学」でベクトルとクォータニオンを 積極的に利用したとあります。 その著作や、グラスマン(1809年-1877年)の広延論を読んだギブスやヘヴィサイドたちは「これベクトルだけの方がよくね?」 と気づいてしまい、ベクトル解析学を捏ね上げていったようです。なんだかこう書くと手柄横取り犯みたいですが、 クォータニオンに至る道を綺麗に舗装していく作業であるとも言えます。 ギブスたちが築き上げたベクトル解析学という巨大な庭園の中央には立派なクォータニオンが鎮座しているのです。 『ハミルトン先生……見ていらっしゃいますか……?』 誰かがこう言ったかどうかは存じ上げません。
その後は我々も知るように、物理などへの応用については比較的分かりやすいベクトル解析学一色になり、 20世紀も終わり近くになって3DCGの分野で注目され、今日のように人口に膾炙するようになるまで ほとんどクォータニオンという単語を耳にする機会は無くなったのです。 そんな20世紀の終わりの時期にクォータニオンへ3DCGの分野から熱い視線を注いでいた日本人たち、彼らのうち一人が何を隠そうこの私でございます。デデーン
いやまあ威張るような事ではないし、僕の知識なんてほぼShi3z氏やDevilman氏の受け売りに僕なりの思い込みや誤りを混ぜ込んだ代物だったんですが。
EMANの物理学に載ってました。さすがEMAN先生。 いつも頼りにしていますが、なんとたった3本の式でいきなりバッサリです。なるほど、聖杯は無かった。 双複素数、分解型四元数、双曲四元数の話も非常に面白い!僕らの手こずっているクォータニオンは四天王のうち最弱…… だったのかもしれないんですね。
まず、クォータニオンの成分同士の乗算をおさらいしましょう。Unityでの表記に準拠して クォータニオン\( (x,y,z,w) = w + x\vec{i} + y\vec{j} + z\vec{k} \)の\(\vec{i}, \vec{j},\vec{k} \) 同士の乗算は以下のように定義されます。 \[\vec{i}\vec{i} = \vec{j}\vec{j} = \vec{k}\vec{k} = \vec{i}\vec{j}\vec{k} = -1,\] \[\vec{i}\vec{j} = -\vec{j}\vec{i} = \vec{k}, \vec{j}\vec{k} = -\vec{k}\vec{j} = \vec{i}, \vec{k}\vec{i} = -\vec{i}\vec{k} = \vec{j}\]
もうここで既に嫌な予感しかしないんですが、「実数軸である\(\vec{1}\)と掛けても軸が変わらないのに、i,j,kと掛けると軸が変わる」「\(\vec{1}^2\)だけ+1」 となんだかWだけ贔屓というか特別枠になってるの?という違和感があります。そもそも複素数は実数同様、 積について可換ですが、クォータニオンは非可換です。 ともかく、各基底要素同士の乗算を表にすると
| 右辺 | ||||
| ↓左辺 | 1 | i | j | k |
| 1 | 1 | i | j | k |
| i | i | -1 | k | -j |
| j | j | -k | -1 | i |
| k | k | j | -i | -1 |
なんだか古き良き時代のテーブル丸出しですが読みやすさ最優先ということでご勘弁願いとうございます。 まず、オレンジの斜めのセルを軸にして転置すると違う表になってしまうということで、積について非可換である事が確認できます。 次に、\(\vec{1}\)との乗算をピンク色のセルにしてみました。 ピンク色のセル同士は線対称になっていてひっくり返せますが、 ピンクでない右下3*3のセル同士は線対称になっているセルとは互いにマイナス同士の値になっているせいで非可換です。 やはりクォータニオンはWだけ特別扱いされているんでしょうか。 そして、積の結果をみると
なんだかすっきりしません。-1の方に注目すると、-1,i,j,kで各3回ずつ出てくるのですが、
1の方に注目すると1,i,j,kで1,3,3,3回現れることになってしまいます。
やはりWだけ特別扱いされていて、「Wと愉快な仲間たち」という扱いで突き進んでいって良い概念なんでしょうか?
以前に四次元ジュリア集合の表示デモを作った時、Wを固定するとジュリア集合は回転体にしかならないが
X,Y,Zのどれかを固定する分にはそうでもなくなるという理由がなんとなく見えてきた気がします。
余談になりますがバイクォータニオンなるx,y,z,w自体が複素数とかいう悪夢のような概念も考えられているようです。
ちらっと書いた双複素数もクォータニオンの仲間というか実はバイコンプレックスです。
数学者というのは悪夢の中をどこまでも平然と突っ走っていく人たちのようで、そうなるとクォータクォータニオン(x,y,z,wがそれぞれクォータニオン)とか
バイクォータバイクォータクォータオクトニオン(8つの成分がそれぞれバイクォータバイクォータクォータニオンであり、
バイクォータバイクォータクォータニオンとはxyzwがそれぞれバイクォータバイクォータニオンであり……以下略)とかも作れるんでしょうか。書くだけで頭痛がしてきました。
何が言いたいのかと言うと一次元だと思っていた「数」を建て増ししまくって無限次元の住人まで作れるのかも?という話でした。違ったらすみません。
複素平面について考えても、-1倍するという操作は180度の回転を示し、i倍は90度の回転を示します。 どういう回転のあり方であっても1倍が「回転しない」という所は変わらないと仮定すると、 このような結果が得られるのは必然なんでしょうか。
HMMNRST氏の記事 によると確かに四次元空間での回転に相当するそうです。 HMMNRST氏の記事は本当に秀逸で以下はただの感想文ですから、実のある話を読みたい方は リンクをクリックして頂いたほうがいいと思いますが、 四次元空間での回転というものがどういうものなのか当初全く想像が付かなかったのです。 三次元の軸に対して軸と垂直な平面上を回る、僕らの意図している回転の他に、 三次元の軸に穴を通したドーナツがめくれ上がるような回転というのも四次元ではあるんですね。 だから、クォータニオンを使った僕らが「おいおい、上手く回してくれよ、変な方向にガタガタ動いてるじゃねえか」 と思っても、「旦那、ちゃんと言われた通り、めくり返してますぜ?」とクォータニオンは言ってたのかもしれません。 僕の、このページは書きかけの段階はクォータニオンは四次元空間とは関係が無く同次三次ベクトルの操作に特化した概念である と結論ありきで書き進めていたのですが、そのまま公開しなくて良かったです。
それにしても2Dから3Dになったときでも相当に四苦八苦したのにこれからさらに4Dとなると 一生楽しめるんじゃないかと思ってしまいますが、別に4Dゲームを作ることを目指しているわけではないので、 四次元から俯瞰する事で三次元に現れる出来事をより簡単に説明することが出来る可能性がある、というアイディアを活かして、 これからのクォータニオン利用に活かすところまで行ければよいのではないかと思いました。 ともかく「三次元までしか知覚できない我々には四次元空間については想像することすら出来ない」という話を どこかで読んだような気がするのですが、訓練することによって四次元空間のイメージを つかめるのだと確信しました。
それにしても、先に述べたようにクォータニオンには双複素数などいくつか仲間が居ますが、 それぞれの違いというのは三次元における右手系・左手系のような違いと考えてしまっていいんでしょうかね?
ニコニコ大百科の四元数についての解説 がコンパクトで分かりやすく秀逸だと思いましたから、以下、極形式でクォータニオンを表示する方法を借りて、説明を続けます。 ベクトル成分の向きを\(\vec{I}\)とする長さ1のクォータニオン\(Q = (\cos\theta,\sin\theta\vec{I}) , |\vec{I}|=1 \)について、\(Q = e^{\vec{I}\theta}\)とも書くことにします。 うーん、コンパクト。
どうしてベクトルを軸回りに回転させる式は\(e^{\vec{I}\frac{\theta}{2}}\vec{V} e^{-\vec{I}\frac{\theta}{2}}\) なのかというところは長らく引っかかるところでしたから、この際に解決しようと。 そもそも\(e^{\vec{I}\theta}\vec{V}\)じゃだめなんですか? というか実際プログラムを書いてグルグル回したら明らかに見てダメな事は分かるんですが、何が、どうダメだというのか? そもそもアレですよ。クォータニオンとベクトルの積を取る時にベクトルの方を同次三次ベクトルとして拡張するじゃないですか。 4つ数がないと積が取れないというのは仕方ない事実として受け入れられますけど、なんで同次三次ベクトルなんですか? 同次になっただけでどうしてクォータニオンと同等に渡り合ったりするんですか?イキりも大概じゃないですか? W=0とかじゃダメなんですか?そっちの方が計算しやすいじゃないですか?なぜ!?どうして??
こぶ茶でも呑んで落ち着いて考えるとしましょう。 まず、クォータニオンと積を取るにあたって同次三次に拡張する理由についてですが、 僕らがデカルト座標を格納するのにいつも使っている三次元ベクトルというのはローカル座標→ワールド座標に変換する時など、 一次変換のときには必ずW=1を足された同次三次ベクトルに代入されてます。忘れていただけで必ずそうなってます。 そうじゃないと平行移動を行列で表現できません。 ですから、クォータニオンと積を取る=クォータニオンによる一次変換を行う時もW=1を足して 同次三次に拡張してから行うというのは自然な話だと思います。別に同次座標系に拘らなくても何かクォータニオンと互いに積を取れるような 4要素のベクトルに出来るような方法があって、なおかつ元の三次元ベクトルに戻せるような方法もセットで考えられると言うならそれを使ったって良いはずなんです。 ていうかぶっちゃけWには(浮動小数型の精度を気にしない限り)何を入れても良いということが後で分かります。 ……と、書いた後で知ったのですが、W=0を代入するという流儀もあるそうです。僕は同次三次に拡張するという理屈が腑に落ちたのでW=1を採用していました。
さあ、\(e^{\vec{I}\frac{\theta}{2}}\vec{V} e^{-\vec{I}\frac{\theta}{2}}\)なる奇妙なサンドイッチについて考えてみましょう。 \(\vec{V}\)を\(\vec{I}\)に対して垂直な成分と水平な成分に分解します。 垂直成分を\(\vec{V_\perp}\)とし、水平成分を\(\vec{V_\parallel}\)とします。\(\vec{V} = \vec{V_\perp} + \vec{V_\parallel}\)です。
まず、ゴールのお手本としてロドリゲスの回転公式をこの形に書き改めると、ベクトル\(\vec{V}\)を軸\(\vec{I}\)周りに\(\theta\)回転させて\(\vec{V'}\)を得たとして、 \[\vec{V'} = \vec{V_\parallel} + \cos\theta\vec{V_\perp} + \sin\theta\vec{I}\times\vec{V_\perp}\] が成り立つことになります。
まず\(e^{\vec{I}\alpha}\vec{V}e^{-\vec{I}\beta}\) = \(e^{\vec{I}\alpha}\vec{V_\perp}e^{-\vec{I}\beta} + \vec{V_\parallel}\)と書きます。 水平成分は回転の影響を受けないから\(e^{\vec{I}\alpha}\vec{V_\parallel}e^{-\vec{I}\beta} = \vec{V_\parallel}\)となります。出し入れ自由です。 そして、\(\vec{V}\)を同次三次に拡張して\((w,\vec{V})\)と書きます。これも分解して\((w,\vec{V}) = (w_\perp,\vec{V_\perp}) + (w_\parallel,\vec{V_\parallel})\)とします。
そうしたら、\(e^{\vec{I}(\alpha+\beta)}(w_\perp,\vec{V_\perp}) = (w_\perp\cos(\alpha+\beta), \cos(\alpha+\beta)\vec{V_\perp} + w_\perp\sin(\alpha+\beta)\vec{I} + \sin(\alpha+\beta)\vec{I}\times\vec{V_\perp})\)
\(\alpha = \beta = \frac{\theta}{2}\)を代入して \[e^{\vec{i}\theta}(w_\perp,\vec{V_\perp}) = (w_\perp\cos\theta,\cos\theta\vec{V_\perp} + w_\perp\sin\theta\vec{I} + \sin\theta \vec{I}\times\vec{V_\perp}) \\ e^{\vec{i}\theta}(w,vec{V}) = (w_\perp\cos\theta + w_\parallel, \vec{V_\parallel} + \cos\theta\vec{V_\perp} + w_\perp\sin\theta\vec{I} + \sin\theta \vec{I}\times\vec{V_\perp})\]
少し頑張って計算しましたが、なんだか惜しいけど違う結果になっていますね…… ベクトル成分だけでも\(w_\perp\sin\theta\vec{I}\)なる余計な項が付いていて、W要素もwくらいになってほしいのに\(w_\perp\cos\theta + w_\parallel\)になっています。 自分で実験用プログラムを書いて動かしながら見てみたのですが、確かにこの式で回転させたサンプルと正しく回転させているサンプルとを比べると W要素をデカくするほど\(\vec{I}\)沿いにズレてしまいます。一見W=0にすると片側から掛けるだけでも正しく回転できそうに見えるのですが、 よく見ろ、そのWには\(_\perp\)がついている!なので、「W=0をセットする流儀に則って」「回転軸と垂直な成分しか無いベクトルを回転させる」 というテストケースを通すと、「共役を右から掛けなくてもいいんじゃね?」と見えてしまうんですね。 さあ、もう片方行ってみましょう。
\[e^{\vec{I}\alpha}\vec{V_\perp}e^{-\vec{I}\beta} = (w_\perp\cos(\alpha-\beta), \cos(\alpha+\beta)\vec{V_\perp} + w_\perp\sin(\alpha-\beta)\vec{I} + \sin(\alpha+\beta)\vec{I}\times\vec{V_\perp})\]
\(\alpha = \beta = \frac{\theta}{2}\)を代入して \[e^{\vec{I}\frac{\theta}{2}}\vec{V_\perp}e^{-\vec{I}\frac{\theta}{2}} = (w_\perp, \cos\theta\vec{V_\perp} + \sin\theta\vec{I}\times\vec{V_\perp}) \\ e^{\vec{I}\frac{\theta}{2}}\vec{V}e^{-\vec{I}\frac{\theta}{2}} = (w, \vec{V_\parallel} + \cos\theta\vec{V_\perp} + \sin\theta\vec{I}\times\vec{V_\perp}) \]
こっちは大分頑張って計算しました。僕がああでもないこうでもないとして3日ほど仕事の後やら途中やらで 式を立てて捏ね回したので計算ミスがあったらすみませんが、これならバッチリな結果じゃないですか? \(\theta\)が半分ずつにされてサンドイッチになっている理由を(4次元空間をイメージしなくてすむ範囲で)後付けで考えるとこんな感じでしょうか?
大分スッキリした気がしますね! ともかく1.が重要なポイントで、三次元ベクトルを回転させる場合はこれが満たされていないと回転とは言えない操作になってしまいます。 W成分がもとの値から書き換えられてしまうという事は、同次座標系で捉えると勝手に拡大・縮小されてしまうという事ですし、 4次元デカルト座標系で捉えると同じ軸回りでも違う回り方をしている(先のHMMNRST氏の記事参照)という事です。 全く同じ計算なのに座標系の捉え方だけで解釈が変わるのって面白くないですか? 意外と「クォータニオンは4次元デカルト座標系の回転」という捉え方から外れて同次三次元座標系で捉えると 普通に図示も出来るしシュールリアルな光景が拝めて楽しいかもしれません。 いずれにしても、同次三次という4要素のベクトルで計算をしているのですから、 僕らは常に4次元デカルト空間を3次元空間に射影したものを(さらにスクリーン平面に射影する作業を経て2次元に落とし込んで) 観察しているという風に考えることも出来ます……というアイディアに基づいて同次座標系の説明を後で書き足したのです。
またゲームを作っているのですが、VFX Graphいじりが何より楽しくていじり倒す過程でクォータニオン熱が高まってしまったので
おもむろに書き連ねてしまいました。歴史を紐解く作業が非常に面白くて、当初はWikipediaからちょっとコピペ引用でさらっと終わるつもりだったのですが、
複素数から始めて関連する人物を時系列にどんどん並べていったらWikipediaの項目だけでも山のように読む必要が出て、
どの項目も非常に楽しくて読み応えがあるものですからゲーム作りは完全にストールして予定よりもずいぶん長く読み書きをしていました。
クォータニオンやベクトルがどういうつもりで作られた概念なのか、それを追うことで今までモヤモヤとしていた部分が随分晴れました。
僕は自分では理系気取りなんですが、どうにもナラティブな部分に引っ張られるもので、論理的には合っててもその数値や式に潜んでいる意図がわからないと
どうにも納得できません。逆に、意図がはっきりすると数値が間違ってても「ああ、そういうことね?うん、いいんでない?」となってしまうんですが。
ですから、僕のような奴は新しい概念に出会ったら、いきなり概念と格闘するんじゃなくてその歴史から辿ればスッキリと腑に落ちるんだと再確認したわけです。
クォータニオンそのものからは外れますが、クォータニオンにはいくつか仲間がいる事もわかりました。 双複素数は積について可換という有り難い?性質を持っています。 4Dマンデルブロ集合やジュリア集合は我々が今用いているクォータニオンではなく、双複素数で計算することが良いのかもしれません。 ともあれ、どんなタイプの四元数で計算しようと絵は出てくるので、ロマン主義的アプローチで「カッコいい絵の出せるヤツが優勝」で良い気もします。 絵を見ることで各四元数の性質について洞察を得る事が重要なのです。 そう思ってVFX Graphでしょうもないボリュームレンダラを作ったので突っ込んでみました。

どう見てもボリュームデータを作っているフラクタル図形じゃなくてSDユニティちゃんが主役です本当にありがとうございました。 現状ではGPUパワーやメモリの問題で解像度が低いのですがボリュームレンダラがあれば(比較的)手軽に 四次元図形を投影できるはずなので四次元空間についてのさらなる洞察を得ることが出来るかもしれません。 問題はVFX Graphがノードベースなものでこういう用途に使おうとすると(僕の作業上の負担という意味で)結構重いということです。 正直に自前でレンダラを書いたほうがいいんじゃ……
Hayase Taku(SANDMAN)